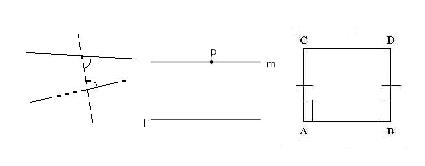
▲유클리드 제5공리와 동치인 정리들 ⓒ 이근무
"첫째 직선 L과 그 위에 있지 않는 점 p가 주어졌을 때 이 직선 L과 점 p가 결정하는 평면 위에서 점 p를 지나고 좌우로 아무리 늘여도 L과 만나지 않는 직선 M을 단 하나 그릴 수 있다." (위 그림의 중간)
제5공리와 동치인 또 하나는 '직각의 정리'이다. 이 정리는 다음과 같다.
네개의 직선 AC, CD, DB, BA 로 만들어진 등각 사다리꼴 모양의 도형 ACDB를 생각한다. BA(혹은 AB)가 밑변이고 AC 와 BD는 AB에 대해서 같은 쪽으로 세운 AB의 수직선이고 길이가 같다. 이 도형은 AC=BD이고 각 ∠CAB 와 각∠DBC는 직각이다. 이 직각의 정리는 평행선의 공리를 쓰지 않아도 감각으로 ∠ACD와 ∠BDC는 직각과 같다는 것을 볼 수 있지만 평행선의 공리를 사용하지 않으면 증명되지 않는다.
따라서 평행선 공리를 가정하면 ∠ACD와 ∠BDC가 직각임을 증명할 수 있으며 역으로 ∠ACD와 ∠BDC가 직각이라고 가정하면 평행선의 공리가 증명된다. 다시 말하면 ∠ACD와 ∠BDC가 직각과 같다는 가정은 평행선의 공리와 동치이다. (위그림의 오른쪽)
유클리드 기하학은 기원전 3세기 <원론> 출간 이후 2200여년간 절대적 진리로 그 권위를 인정 받아 왔다. 유클리드의 기하학 체계가 세상이 영원히 존재하는 필연적 구조로 인식되고 군림하여 왔다.
19 세기의 수학자 로바체브스키(1793~1856)는 이러한 권위에 의지한 기하학적 질서에 대한 도전자였으며 새로운 공간과 우주 질서를 여는 안내자였다. 그는 그 시대까지 절대적 진리라고 믿었던 유클리드의 제5공리와는 모순되는 기하학적 질서를 발견하여 공표하였다.
아래의 그림 왼쪽과 같은 두개의 나팔을 붙인 것과 같은 곡면에서는 유클리드의 제5공준과 동치인 직각의 가설은 만족하지 않는다. 이 경우 제5공리는 부인되며 직각인 두 밑변을 가진 등각사다리꼴인 사변형이 되어 이때에는 직각에서 마주보는 각들은 예각(90도 이하의 각)이 된다. 주어진 직선과 직선 밖의 한 점을 지나며 그 직선에 평행한 직선은 적어도 두개 이상 존재한다. 이러한 기하학을 '로바체브스키 기하학' 또는 '쌍곡 기하학'이라 부른다. 이는 유클리드 기하학의 권위를 깨는 결정적 계기가 되었다.
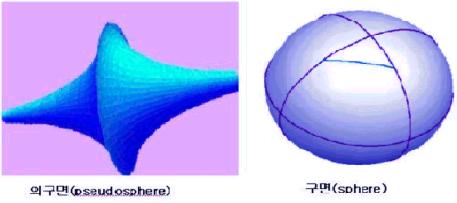
▲의구면과 구면 ⓒ
로바체브스키의 발견 이후 유클리드 제5공리에 대한 도전은 계속되었다. 그 한 예를 들어보면 아래 그림의 오른쪽과 같은 구면에서도 유클리드의 제5공리는 성립하지 않는다. 이 경우에는 직각인 밑변에서 마주보는 각들을 둔각(90도 이상)이 되며 한 점을 지나 주어진 직선과 평행한 직선은 존재하지 않는다. 이런 기하학을 곡면 기하학 또는 리만(1826∼1866)이 발견하였다 해서 리만기하학이라 한다.

▲로바체브스키 ⓒ
유클리드의 제5공리(평행선 공리)는 완전 평면상에서나 성립되는 공간의 특별한 한 경우에만 적용될 수 있는 공리이며(이런 면에서 공리라 부른 것이 적합지 않지만 관습적으로 이렇게 아직도 부르고 있다) 구면이나 의구면 등의 입체들이나 다른 구조들에서는 이 공리는 성립하지 않는다.
이 공리는 세상(지구)을 평면으로 인식했던 유클리드 시대의 세계관과 우주관을 반영하고 있다. 이러한 모순이 2200여년간이나 부정되지 못한 것은 의문을 가지면서도 절대적 권위에 굴종하는 인류 역사의 한 단면을 반영하는 것이다.
덧붙이는 글 | 이기사는 시민의 신문(http://www.ngotimes.net)에 연재중입니다.